লেখচিত্রের সাহায্যে সহজেই সমীকরণের সমাধান বের করা যায়। মনে করি, 2x - 5 = 0 সমীকরণটি সমাধান করতে হবে। সমীকরণের বামপক্ষ 2x - 5 রাশিতে x-এর বিভিন্ন মান বসালে রাশিটির বিভিন্ন মান পাওয়া যায়। লেখচিত্রে প্রতিটি X কে ভুজ এবং রাশিটির মানকে কোটি ধরে একটি করে বিন্দু পাওয়া যাবে। বিন্দুগুলো যোগ করে একটি সরলরেখা অঙ্কিত হবে। সরলরেখাটি যে বিন্দুতে x অক্ষকে ছেদ করে, সেই বিন্দুর ভুজই নির্ণেয় সমাধান। কেননা, x-এর এই মানের জন্য রাশিটির মান 0 হয়, যা সমীকরণের ডানপক্ষের মানের সমান হয়। এ ক্ষেত্রে সমীকরণটির সমাধান ।
উদাহরণ ২। 3x - 6 = 0 সমাধান কর এবং লেখচিত্রে সমাধান প্রদর্শন কর।
সমাধান: 3x - 6 = 0
বা, 3x = 6 [পক্ষান্তর করে]
বা, [উভয়পক্ষকে 3 দ্বারা ভাগ করে]
বা, x = 2
∴ সমাধান: x = 2
লেখচিত্র অঙ্কন: প্রদত্ত সমীকরণ 3x-6=0
x এর কয়েকটি মান নিয়ে 3x - 6 এর অনুরূপ মান বের করি এবং নিচের ছকটি তৈরি করি:
x | 3x-6 | (x, 3x-6) |
2 | 0 | (2,0) |
5 | 9 | (5,9) |
6 | 12 | (6,12) |
লেখচিত্র অঙ্কনের জন্য তিনটি বিন্দু (2,0), (5,9) ও (6,12) নেওয়া হলো।
মনে করি, পরস্পর লম্ব রেখা XOX' ও YOY' যথাক্রমে x-অক্ষ ও y-অক্ষ এবং O মূলবিন্দু।
ছক কাগজে উভয় অক্ষে ক্ষুদ্রতম বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্যকে একক ধরে (2,0), (5,9), (6,12) বিন্দুগুলো স্থাপন করি। তারপর বিন্দুগুলো পরপর সংযোগ করি। লেখচিত্রে একটি সরলরেখা পাই। সরলরেখাটি x-অক্ষকে (2,0) বিন্দুতে ছেদ করে। বিন্দুটির ভুজ হলো 2। সুতরাং প্রদত্ত সমীকরণের সমাধান x = 2 ।
উদাহরণ ৩। লেখচিত্রের সাহায্যে সমাধান কর: 3x - 4 = - x + 4
সমাধান: প্রদত্ত সমীকরণ 3x - 4 = - x + 4
x এর কয়েকটি মান নিয়ে 3x - 4 এর অনুরূপ মান বের করি এবং পাশের ছক-১ তৈরি করি:
∴ 3x - 4 এর লেখের উপর তিনটি বিন্দু (0,-4), (2,2), (4,8) নিই।
x | 3x - 4 | (x, 3x - 4) |
0 | -4 | (0,-4) |
2 | 2 | (2,2) |
4 | 8 | (4,8) |
ছক-১
আবার, x এর কয়েকটি মান নিয়ে - x + 4 এর অনুরূপ মান বের করি এবং পাশের ছক-২ তৈরি করি:
∴ -x + 4 এর লেখের উপর তিনটি বিন্দু (0,4), (2,2), (4,0) নিই।
মনে করি, পরস্পর লম্ব রেখা XOX' ও YOY' যথাক্রমে x-অক্ষ ও ৮-অক্ষ এবং মূলবিন্দু। এখন, ছক-১ এ প্রাপ্ত (0,-4), (2,2), (4, 8) বিন্দু তিনটি স্থাপন করি এবং এদের পরপর সংযোগ করি।
x | -x + 4 | (x, -x + 4) |
0 | 4 | (0,4) |
2 | 2 | (2,2) |
4 | 0 | (4,0) |
ছক-২
(0,4), (2, 2), (4,0) বিন্দু তিনটি স্থাপন করি ও এদের পরপর সংযোগ করি। এক্ষেত্রেও লেখচিত্রে একটি সরলরেখা পাই।
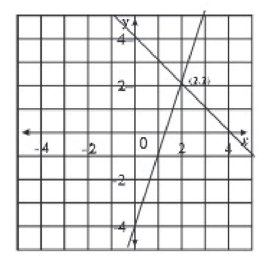
লক্ষ করি, সরলরেখা দুটি পরস্পর (2,2) বিন্দুতে ছেদ করেছে। ছেদবিন্দুতে 3x-43-x+4 এর মান পরস্পর সমান। সুতরাং, প্রদত্ত সমীকরণের সমাধান হলো (2, 2) বিন্দুতে ভুজের মান, অর্থাৎ x = 2 ।
কাজ: নিচের সমীকরণগুলোর সমাধানের লেখচিত্র আঁক। ১। 2x-1=0 ২।3x+5=2 |
common.read_more
common.or
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
